Simons semester 2024
“Knots, homologies and physics” is a research program organized within the “Simons semester” series from March 1 until June 30, 2024. It is devoted to the analysis of the relations between knot theory and physics. The program is hosted at the Institute of Mathematics, Polish Academy of Sciences, and co-organized by the Faculty of Mathematics, Informatics and Mechanics, and Faculty of Physics, University of Warsaw. The program includes two workshops, an advanced school, and other lecture series and seminars by renowned mathematicians and physicists.
For details how to register and other practical information see here.
Here you can find the YouTube channel with lectures from the semester
Organizers
Maciej Borodzik (University of Warsaw and Polish Academy of Sciences)
Piotr Kucharski (University of Warsaw)
Bartłomiej Lewandowski (University of Warsaw)
Jakub Paliga (University of Warsaw)
Wojtek Politarczyk (University of Warsaw)
Piotr Sułkowski (University of Warsaw)
Program
(Almost) weekly seminars
Dates: Mondays (unless otherwise stated), 11:00
Place: Institute of Mathematics, Polish Academy of Sciences (Śniadeckich 8, Warsaw), lecture room 403
March 4
The first welcome and organizational meeting
March 11
Seminar speaker: Sungkyung Kang (Oxford University)
Title: Invariant knot Floer homology of satellites and the invariant splitting principle
Abstract: Involutive knot Floer homology, a refinement of knot Floer theory, is a powerful knot invariant which was used to solve several long-standing problems, including the one-is-not-enough result for 4-manifolds with boundary. In this talk, we show that if the involutive knot Floer homology of a knot K admits an invariant splitting, then the induced splitting of the knot Floer homology of P(K), for any pattern P, can be made invariant under its \iota_K involution. As an application of this “invariant splitting principle”, we construct an infinite family of examples of pairs of exotic contractible 4-manifolds which survive one stabilization, and observe that some of them are potential candidates for surviving two stabilizations. This is an ongoing work with Gary Guth.
April 8
Seminar speaker: Alessio di Prisa (Scuola Normale Superiore)
Title: Solvability of concordance groups and Milnor invariants
Abstract: In this talk I will introduce the notions of concordance for several knotted objects in the 3-space, namely strongly invertible knots, theta curves and string links, and I will explain how the respective concordance groups of these objects are related to one another. Using Milnor invariants, I will prove that the concordance group of 2-string links is not solvable. Exploiting the close relation between the objects mentioned above, it follows that the equivariant concordance group of strongly invertible knots and the cobordism group of theta curves are also not solvable. Finally, I will show how these results can be used to answer a conjecture due to Kuzbary regarding the solvability of the quotient of the concordance group of n-string links modulo pure braids. Join work with G. Framba.
April 29
Seminar speaker: Alberto Cavallo (IMPAN)
Title: Transverse links in Stein fillable contact 3-manifolds
Abstract: We study the behavior of different versions of the Ozsváth-Szabó tau-invariant for holomorphically fillable links in Stein domains. More specifically, we relate the Hedden’s version of the invariant, which needs the assumption that our links live in a contact 3-manifold with non-vanishing contact invariant, with the one introduced by Grigsby, Ruberman and Strle, which on the other hand only depends on the pair link-Spin^c 3-manifold and is then a purely topological invariant. This is joint work with Antonio Alfieri. The main goal of the talk is to describe how our work allows us to recover results about properly embedded holomorphic curves, such as the slice-Bennequin inequality and the relative Thom conjecture, and to find new restrictions on the topology of Stein fillings of certain 3-manifolds. In particular, we show that a Brieskorn 3-sphere, with its canonical orientation, never bounds a rational homology 4-ball Stein filling; confirming a conjecture of Gompf.
May 23, 12:00 (at IMPAN in seminar room 106!)
Seminar speaker: Diego Santoro (University of Vienna)
Title: Taut foliations from knot diagrams
Abstract: Taut foliations have been a classical object of study in 3-manifolds theory. Recently, new interest in them has come from the investigation of the so-called “L-space conjecture”, that predicts that Heegaard Floer L-spaces can be characterised as those 3-manifolds that do not admit coorientable taut foliations. A possible approach to the study of this conjecture is by analysing surgeries on knots and links.
Most of the techniques employed for constructing taut foliations on Dehn surgeries usually make use of some special property of the exterior of the link (e.g. fiberedness). In this talk I will describe a procedure for constructing taut foliations that only makes use of diagrammatic properties of the knot.
June 24, 11:00
Seminar speaker: Luigi Guerrini (University of Warsaw)
Title: Defect Topological Correlators in 3D Supersymmetric Theories
Abstract: Supersymmetric theories provide a fruitful arena for interactions between physics and math. One notable example is the description of correlation functions of supersymmetric operators through precise algebraic structures. I will present an example of this in 3D superconformal field theories. In particular, twisting a specific family of supersymmetric operators restricted to a line yields a non-trivial 1D topological field theory. The corresponding operator algebra will be a quantization of the untwisted ring structure. I will provide an overview of the construction and extend it on the physics side by adding line operators. As an application, I will use localization to compute some correlators in an example relevant to the AdS/CFT correspondence and suggest a possible interpretation as gravitons scattering off M2 branes.
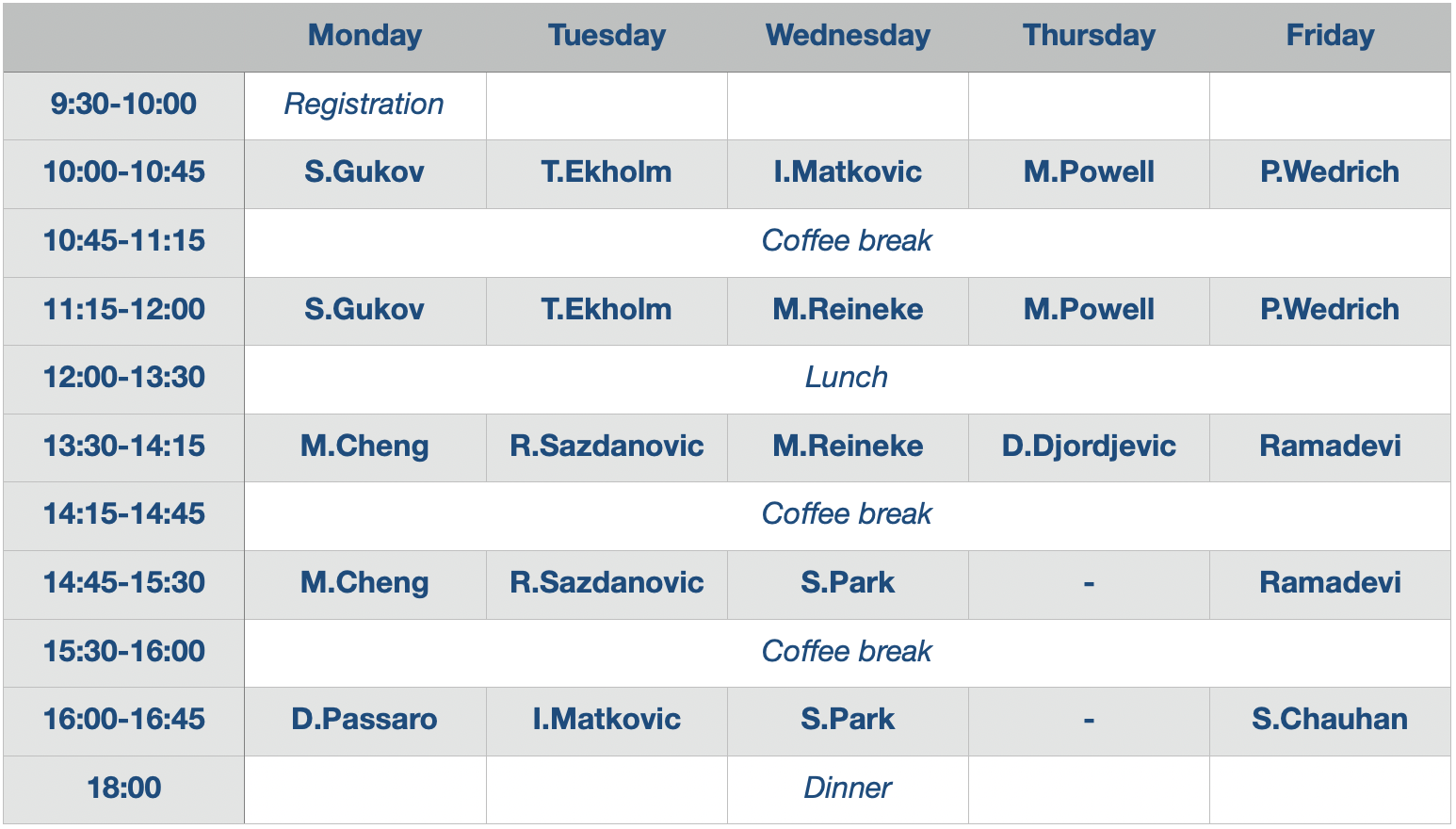
Learning workshop: Knots, homologies and physics (March 18-22)
Dates: March 18-22, 2024
Place: University of Warsaw – Faculty of Mathematics, Informatics, and Mechanics (Banacha 2), lecture room 2180
Deadline for registration: February 15, 2024
Speakers: Sachin Chauhan, Miranda Cheng, Dusan Djordjevic, Tobias Ekholm, Sergei Gukov, Irena Matkovic, Sunghyuk Park, Davide Passaro, Ramadevi Pichai, Mark Powell, Markus Reineke, Radmila Sazdanovic, Paul Wedrich
Informal workshop dinner: Wednesday, March 20, 18:00, restaurant Shuk (address: Grójecka 107)
Titles and abstracts
Sachin Chauhan (Indian Institute of Technology, Bombay)
Title: Refined Gukov-Pei-Putrov-Vafa (GPPV) Conjecture
Abstract: GPPV conjecture relates the two quantum invariants of closed 3-manifolds. On one side we have Witten-Reshetikhin-Turaev (WRT) invariant and on the other side, the q-series valued invariant (also known as Z-hat). In this talk, I will present a more refined version of this conjecture by studying it for SU(N)/Z_m group, for N divisible by m.
Dusan Djordjevic (University of Belgrade)
Title: A gentle introduction to knots and physics: from early days to knots-quivers correspondence and generalizations
Abstract: We will give a highly biased review of the relation between knots and physics, culminating our discussion with the knots-quivers correspondence. By working out examples, we will review some basic facts about knot theory, as well as tackle some original ongoing research.
Tobias Ekholm (Uppsala University)
Title: Knot invariants and skein valued open Gromov-Witten invariants
Abstract: We describe how skein valued counts of holomorphic curves lead to deformation invariant open Gromov-Witten theory. As an application we derive rather simple recursion relations for all colored HOMFLYPT of the unknot and Hopf link.
Sergei Gukov (Caltech)
Title: What do we want from categorification and non-perturbative complex Chern-Simons, and why?
Abstract: This will be a gentle introduction – guided by “Why?” questions – into several topics of recent work that quickly converge toward a common goal. The big overarching goal is to build a bridge between low-dimensional topology (think of the Poincare conjecture, the slice-ribbon conjecture, etc.) and quantum topology (think of many quantum invariants of knots and 3-manifolds). I will explain why one of the most promising paths towards this Big goal requires categorification of quantum 3-manifold invariants and will offer a candidate for “Khovanov homology of 3-manifolds” that is rooted in non-perturbative formulation of complex Chern-Simons theory and in integrality of DT-type invariants.
Irena Matkovic (Uppsala University)
Title: Heegaard Floer homology and contact structures
Abstract: I will review both the applications of Heegaard Floer homology to 3-dimensional contact topology, and contact topology to Heegaard Floer homology. The talk wishes to give an overview of the subject, including results and arguments of many researchers.
Sunghyuk Park (Harvard University)
Title: Towards invariants of 3-manifolds from quantum groups at generic q
Abstract: Motivated by the categorification problem of quantum invariants of 3-manifolds, S. Gukov, D. Pei, P. Putrov and C. Vafa conjectured the existence of a q-series-valued invariant of 3-manifolds. This program was further developed by S. Gukov and C. Manolescu who extended this conjecture to knot complements and gave conjectural surgery formulas. I will give an overview of this program and discuss how this invariant can be defined for a large class of link complements, using representations of quantum groups at generic q.
Ramadevi Pichai (Indian Institute of Technology, Bombay)
Title: Computational status of knot polynomials
Abstract: First, I will give a pedagogical introduction to the elegant tools giving knot polynomials. Then, I will present how these polynomials can address `knot classification’ as well as obtaining three-manifold invariants. The extent to which explicit computation is possible will be highlighted.
Mark Powell (University of Glasgow)
Title: Simple spines of knot traces
Abstract: A knot trace is a 4-manifold obtained by attaching a single 2-handle to the 4-ball along a knot. A simple spine for a knot trace is a locally flat embedded 2-sphere such that the embedding is a homotopy equivalence, and the fundamental group of the complement is abelian. With Feller-Miller Nagel-Orson-Ray, and in two projects with Orson, we characterised exactly when knot traces admit simple spines, and showed that any two are isotopic. I will explain these results and an outline of how they are proven.
Markus Reineke (Ruhr-Universität Bochum)
Title: (Refined) Donaldson-Thomas invariants of symmetric quiver
Abstract: We define (refined) Donaldson-Thomas invariants of symmetric quiver and discuss several of their interpretations in terms of moduli spaces and Cohomological Hall algebras.
Paul Wedrich (Universität Hamburg)
Title: From link homology to TQFTs
Abstract: Skein theory offers several plausible strategies for extending link homology theories, such as Khovanov homology, to topological quantum field theories in 4 or 5 dimensions. In this talk, I will focus on a categorified analog of a TQFT of Turaev-Viro type. Joint work with Matthew Hogancamp and David Rose.
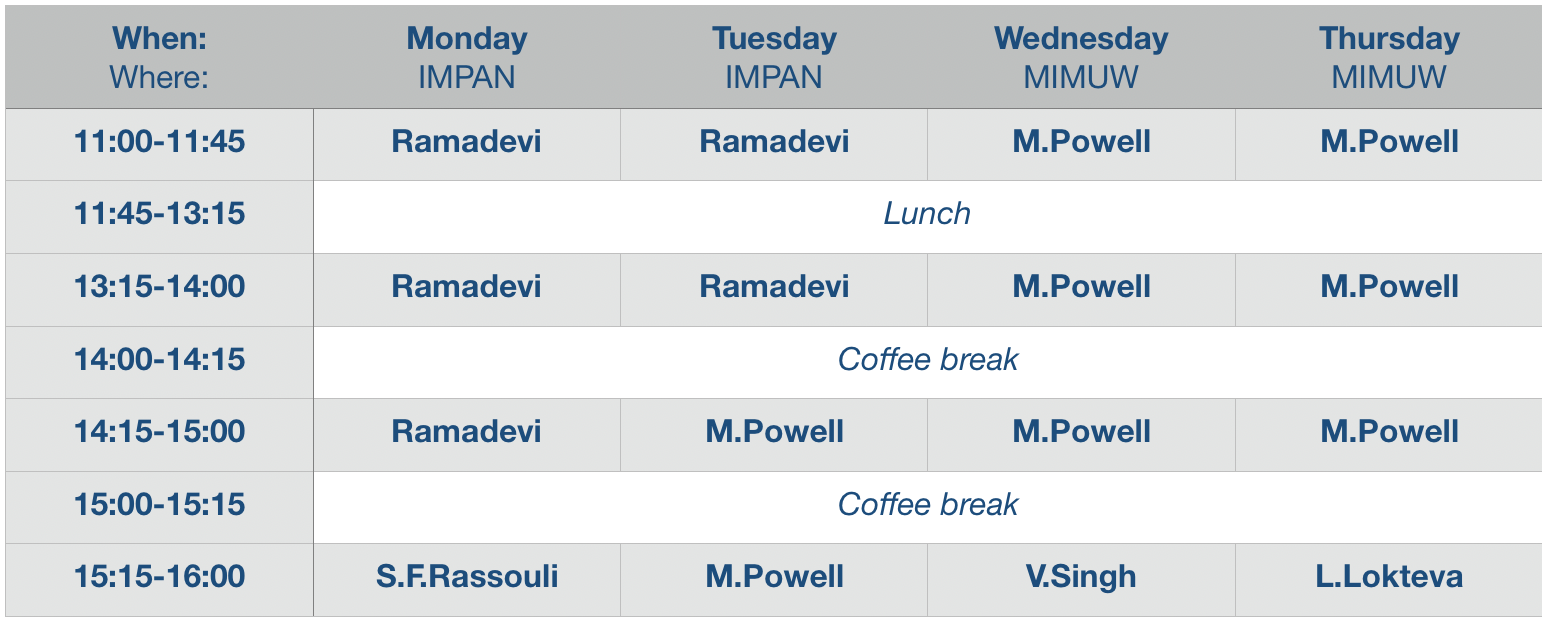
Lecture series (March 25-29)
Dates: March 25-29, 2024
Place:
– Monday and Tuesday: IMPAN = Institute of Mathematics, Polish Academy of Sciences (Śniadeckich 8, Warsaw), lecture room 321
– Wednesday and Thursday: MIMUW = Faculty of Mathematics, Informatics and Mechanics (Banacha 2, Warsaw), lecture room 2180
Lisa Lokteva (Uppsala University)
Title: New Examples of Graph Manifolds Bounding Rational Homology Balls
Ramadevi Pichai (Indian Institute of Technology Bombay)
Title: Chern-Simons Field Theory Invariants: Knots, Links and Three-Manifolds
Mark Powell (University of Glasgow)
Title: Symmetries of 4-manifolds
Sayyed Rassouli (University of Nottingham)
Title: Topological evolution of time in Unimodular Gravity
Vivek Kumar Singh (NYU, Abu Dhabi)
Title: Asymptotics in the invariants of weaving knots W(3,n)
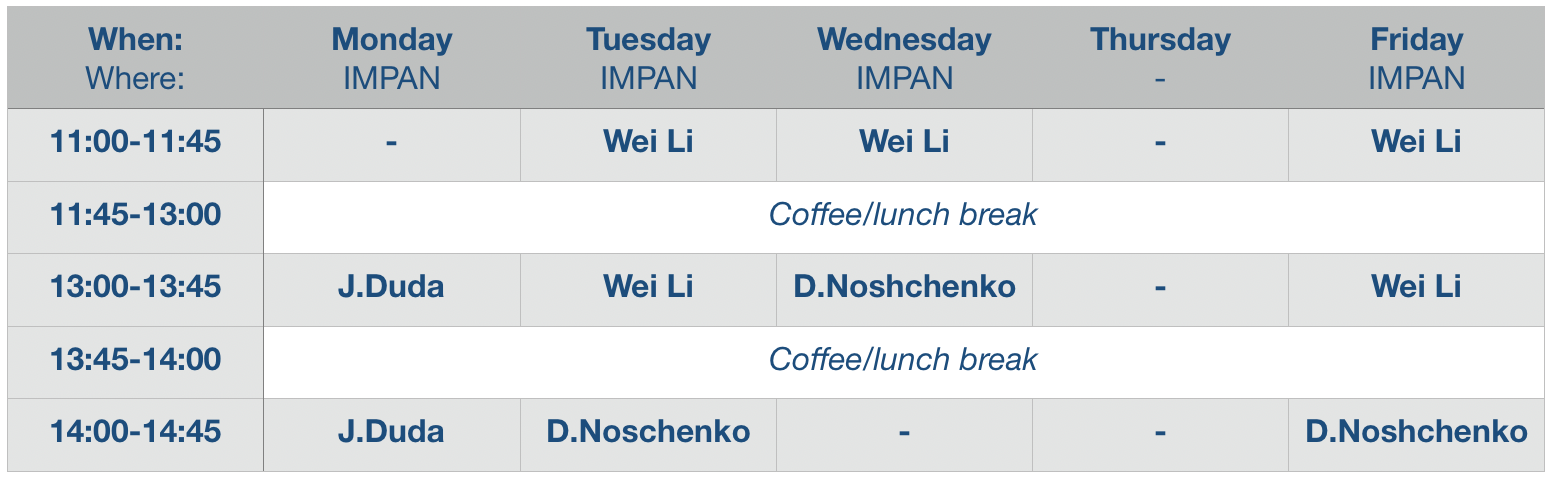
Lecture series (April 22-26)
Dates: April 22-26, 2024 (no lectures on Thursday!)
Place: IMPAN = Institute of Mathematics, Polish Academy of Sciences (Śniadeckich 8, Warsaw), lecture room 321
Jarosław Duda (Jagiellonian University)
Title: Exploring resemblance between topological charges/vortices/knots and particle physics
Wei Li (Chinese Academy of Sciences)
Title: Introduction to quiver BPS algebras
Dmitry Noshchenko (Dublin Institute for Advanced Studies)
Title: Quivers, Nahm sums and hidden symmetries in knot homologies
Note: these lectures will be broadcasted online in the lecture hall
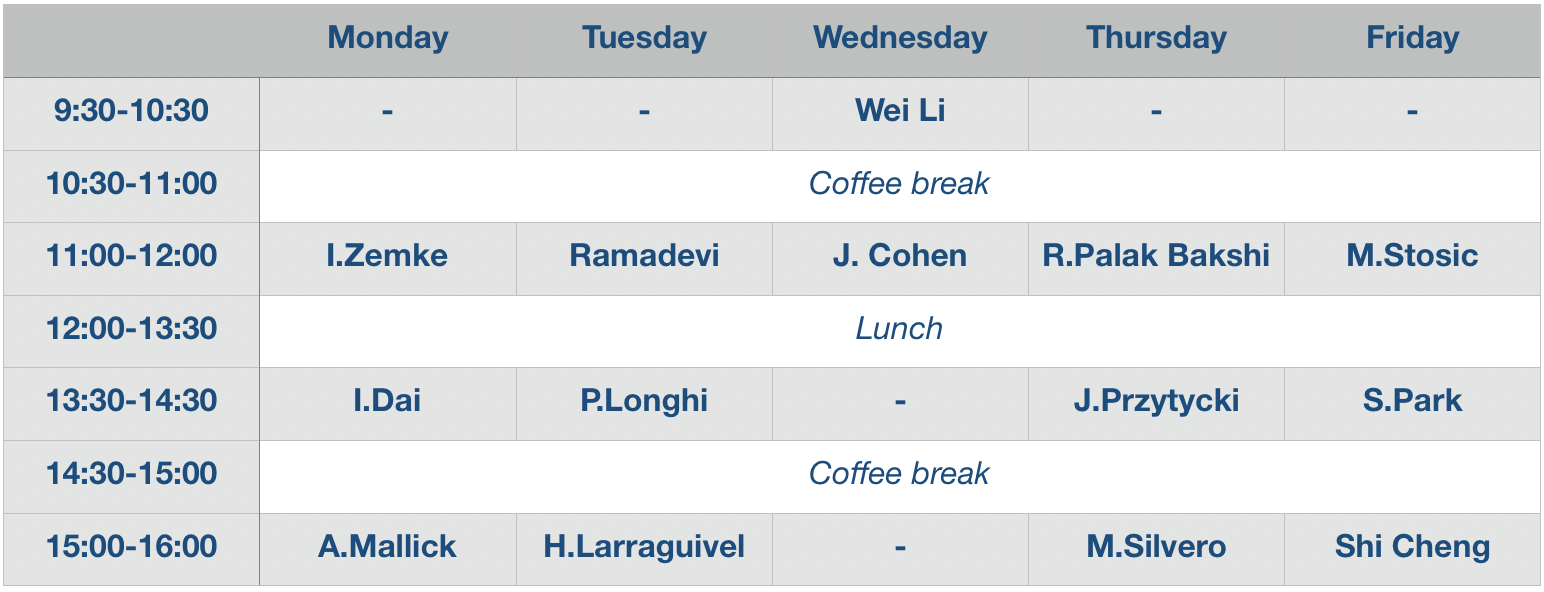
Summary workshop: Knots, homologies and physics (May 6-10)
Dates: May 6-10, 2024
Place: Institute of Mathematics, Polish Academy of Sciences (Śniadeckich 8, Warsaw), lecture room 321
Deadline for registration: March 31, 2024
Speakers: Shi Cheng, Jesse Cohen, Irving Dai, Helder Larraguivel, Wei Li, Pietro Longhi, Abhishek Mallick, Rhea Palak Bakshi, Sunghyuk Park, Ramadevi Pichai, Józef Przytycki, Marithania Silvero, Marko Stosic, Ian Zemke
Titles and abstracts
Shi Cheng (Fudan University)
Title: Quivers, 3d gauge theories and three manifolds
Abstract: We are working to propose an intuitively physical and geometric interpretation for knots-quivers correspondence. It seems to be a long journey to achieve this. We have some progress on the relations between quivers encoding DT-invariants, 3d N=2 gauge theories with matters, and three manifolds with Ooguri-Vafa defects. It turns out that equivalent quivers are Seiberg dualities and Kirby moves. We will show the dictionary between quivers, gauge theories and geometries.
Jesse Cohen (University of Hamberg)
Title: Bordered Floer theory, Hochschild homology, and links in S^1\times S^2
Abstract: An early paper of Ozsváth–Szabó establishes the existence of a spectral sequence from the reduced Khovanov homology of the mirror of a link to the Heegaard Floer homology of its branched double cover. We will describe an analogue of this spectral sequence from Rozansky’s categorified stable SU(2) Witten–Reshetikhin–Turaev invariant of links in S^1\times S^2 to the Hochschild homology of an A_\infty-bimodule defined using bordered Heegaard Floer homology. Along the way, we will see that the (differential) algebras over which these bimodules are defined are nontrivial A_\infty-deformations of Khovanov’s arc algebras.
Irving Dai (University of Texas, Austin)
Title: Z-Disks in CP^2
Abstract: We embark on an explicit enumeration of locally flat Z-disks in CP^2 with boundary a fixed knot K. As a special case, we show that if K has quadratic Alexander polynomial, then K bounds 0, 1, 2, 4, or infinitely many Z-disks in CP^2 (up to topological isotopy rel boundary). We then discuss some related problems in the smooth category. This is joint work with Anthony Conway and Maggie Miller.
Helder Larraguivel (Jagiellonian University)
Title: How many quivers does a knot have?
Abstract: The knots-quivers correspondence aims to pack the whole infinite sequence of colored knot invariants into a symmetric quiver, and finite homology generators. However, for the same knot we usually find a huge set of equivalent quivers all yielding the same knot invariants. In this talk I will present the result of joint work on how we classified equivalent quivers using symmetries of their motivic generating series. Also, I show the set of equivalent quivers is best visualized as a permutohedron graph. Finally, I will discuss what these symmetries imply for invariants of symmetric quivers themselves, beyond the knots-quiver correspondence.
Wei Li (Chinese Academy of Sciences)
Title: Algebras for Knots
Abstract: I will first review the quiver Yangian algebras and their representations for arbitrary quivers and potentials. Then I will explain their relations to knots via the knot-quiver correspondence. Finally, I will discuss a gluing construction for some of these algebras and its connection to knots that does not employ quiver.
Pietro Longhi (Uppsala University)
Title: Quiver structures of knot invariants, open strings, and recursion
Abstract: Generating series of HOMFLY-PT polynomials colored by symmetric representations have been found to coincide with partition functions of motivic Donldson-Thomas invariants of symmetric quivers, after a suitable identification of variables. I will discuss an interpretation of this relation based on string theory, where quivers encode interactions of M2 branes mediated by an M5 brane. Invariance of this picture under deformations leads to a generalization of the knots-quivers correspondence corroborated by wall-crossing type phenomena associated with skein relations among M2 brane boundaries. If time permits, a generalization to multiple M5 branes will be discussed. Based on joint works with Ekholm and Kucharski and ongoing work with Ekholm and Nakamura.
Abhishek Mallick (Rutgers University)
Title: Detecting corks
Abstract: Corks are fundamental to the study of exotic smooth structures on 4-manifolds. In this talk we will discuss how to use Heegaard Floer homology to detect corks. We will then describe some new examples of corks which partially address a question posed by Gompf. This is joint with Irving Dai and Ian Zemke.
Rhea Palak Bakshi (ETH Zurich)
Title: On the structure of skein modules
Abstract: Skein modules were introduced by Józef H. Przytycki as generalisations of the Jones and HOMFLYPT polynomial link invariants in the 3-sphere to arbitrary 3-manifolds. The Kauffman bracket skein module (KBSM) is the most extensively studied of all. However, computing the KBSM of a 3-manifold is known to be notoriously hard, especially over the ring of Laurent polynomials. With the goal of finding a definite structure of the KBSM over this ring, several conjectures and theorems were stated over the years for KBSMs. We show that some of these conjectures, and even theorems, are not true. In this talk I will briefly discuss a counterexample to Marche’s generalisation of Witten’s conjecture. I will show that a theorem stated by Przytycki in 1999 about the KBSM of the connected sum of two handlebodies does not hold. I will also give the exact structure of the KBSM of the connected sum of two solid tori and show that it is isomorphic to the KBSM of a genus two handlebody modulo some specific handle sliding relations. Moreover, these handle sliding relations can be written in terms of Chebyshev polynomials.
Sunghyuk Park (Harvard University)
Title: 3d quantum trace map
Abstract: I will speak about my recent joint work with Sam Panitch constructing the 3d quantum trace map, a homomorphism from the Kauffman bracket skein module of an ideally triangulated 3-manifold to its (square root) quantum gluing module, thereby giving a precise relationship between the two quantizations of the character variety of ideally triangulated 3-manifolds. Our construction is based on the study of stated skein modules and their behavior under splitting, especially into face suspensions.
Ramadevi Pichai (Indian Institute of Technology, Bombay)
Title: Knots, topological strings and quivers
Abstract: I will briefly summarize knot invariants. Then, I will discuss their appearance within topological string context. Finally, I will present our works on knot-quiver correspondence.
Józef Przytycki (George Washington University, Washington)
Title: From the Kauffman and Dubrovnik polynomials to cubic skein modules and beyond
Abstract: The study of linear and quadratic skein modules over the last thirty-seven years has lead to a very rich skein theory that is connected to many disciplines of mathematics and physics, such as algebraic geometry, hyperbolic geometry, Topological Quantum Field Theories (TQFT), and statistical mechanics. There is, however, another class of skein modules with more parameters than the linear and quadratic cases which, save for a few exceptions, have been largely neglected until now. The cubic skein module is the first object in this class which awaits exploration. This is a joint work with Mathathoners VIII.
Marithania Silvero (University of Seville)
Title: Detecting positivity from link homology
Abstract: Khovanov homology is a link invariant which categorifies Jones polynomial. In this talk we present several results concerning Khovanov homology of fibered positive links; in particular, we extend the result by Stosic stating that braid positive links have vanishing Khovanov homology in homological grading 1. We also show how our results can be helpful to detect positivity of certain links. Finally, we explore Khovanov homology of certain cable links and present computational data suggesting that the above result can be extended to L-space knots. This is joint work with M. Kegel, N. Manikandan and L. Mousseau.
Marko Stosic (Instituto Superior Tecnico, Lisbon)
Title: Knots-quivers correspondence: generalizations and combinatorics
Abstract: In this talk I will present basic ideas of knots-quivers correspondence, both in its original form, as well as its extensions and generalizations. Somewhat surprisingly, these correspondences also turned out to have many interesting applications in enumerative combinatorics, including counting of lattice paths and Schröder paths. We will show some of the more recent results, including the ones that are related to quivers with higher level generators.
Ian Zemke (Princeton University)
Title: L-space links and formality
Abstract: A well-known result of Ozsvath and Szabo describes the knot Floer complex of an L-space knot in terms of its Alexander polynomial. The family of L-space knots includes all algebraic knots. The situation of L-space links is comparably less understood. We will describe a conjectural description of the link Floer complex, as well as proof of this conjecture for plumbed L-space links (this family includes all algebraic links) as well as 2-component L-space links. The case of plumbed L-space links is joint with M. Borodzik and B. Liu, and the case of 2-component L-space links is joint work in progress with D. Chen and H. Zhou. The case of 2-component L-space links has applications towards computations of certain satellite operators in Heegaard Floer theory.
Public lecture (May 13)
Date and time: May 13, 2024, 18:00
Place: Faculty of Physics, University of Warsaw (Pasteura 5, Warsaw), lecture room 0.03
See also lecture website and Facebook event
Prof. Sergei Gukov
Mathematics as a game
More details
Advanced school: Insights into knots, homologies and physics (May 13-17)
Dates: May 13-17, 2024
Place:
– Monday and Thursday: IMPAN = Institute of Mathematics, Polish Academy of Sciences (Śniadeckich 8, Warsaw), lecture room 321
– Tuesday, Wednesday and Friday: MIMUW = Faculty of Mathematics, Informatics and Mechanics (Banacha 2, Warsaw), lecture room 2180
– Public lecture, Monday, 18:00: Faculty of Physics (Pasteura 5), lecture room 0.03
Deadline for registration: April 14
Irving Dai (Stanford University)
Title: Floer homology and symmetries of knots and manifolds
Sachin Grover (Harish-Chandra Research Institute, Allahabad)
Title: Duality defects in D_n-type Niemeier Lattice CFTs
Sergei Gukov (Caltech and Dublin IAS)
Title: Categorification of quantum invariants: from knots to 3-manifolds
Józef Przytycki (George Washington University)
Title: Introduction to Skein Modules and their Khovanov type categorification
Matthew Stoffregen (Michigan State University)
Title: A tour of monopole Floer Spectra
Marko Stosic (Technical University of Lisbon)
Title: Knot quantum invariants, graphs, and combinatorics
Online lecture course (April 3 – July 12)
Paul Wedrich (Hamburg University)
Online course: Master level course on knot homology
Wednesdays, 16:15-17:45, April 3 – July 10
Fridays, 12:15-13:45, April 5 – July 12
Lecture course website
Information for participants
Visiting & registration
In order to register and attend some part of the semester, or to attend one of the workshops listed above, please fill in this form. Please fill it in only once (and mark relevant events), even if you are going to attend more than one event!
There is a limited funding to support participation of younger participants in lecture series and advanced schools (see the dates in the program!) – if you need some support for your visit please mention this upon registration.
Note that during the semestr there will be a few periods with holidays, when the academic institutions are closed and there will be no lectures or other activities:
– Easter break: March 29 – April 1
– May holidays: May 1-5 (with Labour Day on May 1st and Constitution Day on May 3rd)
– Corpus Christi: May 30 – June 2 (the official holiday on Thursday is usually followed by the long weekend)
Location & contact
Various activities during the semester (lectures, workshops, seminars) will be held:
– at the Institute of Mathematics, Polish Academy of Sciences (street address: Śniadeckich 8)
– University of Warsaw, Faculty of Mathematics, Informatics, and Mechanics (Banacha 2)
– Faculty of Physics, University of Warsaw (Pasteura 5)
Contact: knot_simons@impan.pl
Travel & transport
Warsaw Chopin Airport – the main airport serving Warsaw. It is located within the city limits, 10 km from the city center, which you can easily reach by a few city buses, a train line, and a taxi.
Warsaw Modlin Airport – another airport, mainly serving budget airlines, located 35 km from the city . It takes around 50 minutes to get to the city center, either by bus and train or a taxi.
Warszawa Centralna Railway Station – the main railway station located in the city center, also serving international trains.
Public transport in Warsaw – the city has a vast transportation network, which includes buses, metro, and trams. You can buy tickets for a single trip (up to either 20 or 75 minutes, with transfers allowed), or multi-day tickets.
Warsaw Public Bike “Veturilo” – one of the largest urban bike systems in Europe. It is a good complement to public transport in Warsaw and allows quick navigation through our city, with over 300 stations and more than 4500 bicycles available. You can register and use at little or (for short enough rides) no cost.
Accommodation
Here are some (relatively) nearby hotels in which participants might choose to stay. For more options you can check Google maps, booking.com, etc.
Guest/hotel rooms at Institute of Mathematics, Polish Academy of Sciences (contact us directly)
Hera – guesthouse of the University of Warsaw (budget option)
Campanile Warszawa (***)
MDM Hotel (***)
Radisson Blue Sobieski (****)
Polonia Palace (****)
Acknowledgments